| Vond Leonardo da Vinci de
fractale wiskunde uit? Sterke aanwijzingen hiervoor treffen we aan
in de Codex Leicester. Leonardo da Vinci werd in 1452 geboren in het
plaatsje Vinci niet ver van Florence. In oude teksten wordt hij beschreven als 'Leonardo di ser Piero da Vinci', Leonard de zoon van Piero uit Vinci. Hij leerde schilderen in Florence maar hij werkte ook als militair architect en ingenieur voor Cesare Borgia. Zijn carriŤre zette hij voort in Milaan in dienst van hertog Ludovico Sforza, daarna in Rome en later in Frankrijk, waar hij werkte voor koning Frans I. In 1519 stierf hij in Amboise. Leonardo werd bekend als schilder, maar hij was veel meer. Beroemd werd hij vooral door kunstwerken zoals de 'Mona Lisa' en de muurschildering 'Het laatste avondmaal'. Als 'uomo universale', algemeen ontwikkeld mens, als universele geest, was hij het grootste genie van de renaissance. |
 |
| Wij bespreken hem hier vanwege
zijn wetenschappelijke ideeŽn. Modern is dat hij zijn aantekeningen
baseerde op waarnemingen en daarmee een voorloper werd van het
empirisme. Hij verzamelde kennis op bijna ieder wetenschappelijk
gebied en deed daar ontdekkingen die nog altijd niet allemaal
ontraadseld zijn. Zo maakte hij op wiskundig gebied notities over de
constructie van regelmatige veelhoeken en de kwadratuur van de
cirkel. Belangrijk is ook zijn ontleding van het menselijk lichaam, deels ten dienste van de kunst maar gedeeltelijk ook uit wetenschappelijke belangstelling. In de natuurkunde deed hij onderzoekingen naar mechanica, optiek en hydraulica. Het is vrij zeker dat hij de wet van Pascal heeft ontdekt voordat de naamgever die formuleerde. Deze wet houdt in dat de druk die op een vloeistof in een gesloten ruimte wordt uitgeoefend, door die vloeistof onverminderd naar alle delen van die vloeistof wordt doorgegeven. Omdat hij een camera obscura gebruikte, nemen sommige geleerden wel aan dat hij daarmee vorm heeft gegeven aan de lijkwade van Turijn. Het portret op de lijkwade zou zijn eigen portret zijn, maar dat is op grond van de C-14 datering minder waarschijnlijk. Daarnaast deed hij ook allerlei uitvindingen zoals een tank, een onderzeeŽr en een helikopter. Verder ontwierp hij moderne bruggen, een apparaat met tandwielen dat vermoedelijk een rekenmachine is op de wijze van Babbage en een vliegtuig. |
 |
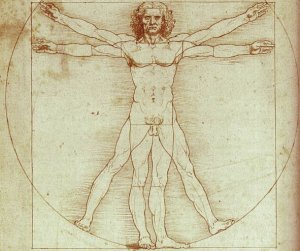
Getallen Een belangrijk deel van zijn ontdekkingen en uitvindingen is neergelegd in zijn aantekeningenboeken die hij noteerde in spiegelschrift, een soort geheimschrift. Voorbeelden daarvan zijn de Codex Atlanticus en de Codices Madrid I en II. Bill Gates telde bijna 31 miljoen dollar neer voor de aankoop van de Codex Leicester. Ook in de schilderijen van Leonardo was een code verstopt, zoals de boodschap die door Dan Brown in 'De Da Vinci code' is ontrafeld. Daaruit zou blijken dat naast Jezus op het 'Het laatste avondmaal' niet de apostel Johannes zit, maar Maria Magdalena die met Jezus getrouwd was. In de uitbeelding van het menselijk lichaam die bekend staat als de Vitruvische mens verborg Leonardo de ontdekking van de verhouding 1: 1,618. Bij voorbeeld: de verhouding van de afstand van de pols tot de vingertop tot de afstand van de elleboog tot de pols tot is 1: 1,618. Op allerlei plekken in het menselijk lichaam op deze afbeelding komt die verhouding terug. Op deze zogeheten 'Goddelijke verhouding' of Gulden snede zijn veel verschijnselen in de natuur gebaseerd. Dit getal is te vinden in de kunst, in de relatie tussen verschillende hartslagen, in de beschrijving van de Ark van Noach en de vorm van een zeeschelp. We zien het zelfs in de ideale maten van het menselijk gezicht. Bij het gebruik van een getal tussen 1 en 2 liep hij vooruit op latere ontdekkingen, maar hij was niet de eerste. De Pythagorese broederschap wist al dat sommige getallen tussen 1 en 2 zoals wortel 2 een bijzondere waarde hadden. Zij kwamen echter niet toe aan fractale meetkunde. In de dertiende eeuw deed Fibonacci een poging om 1,618 konijnen te fokken, maar zonder succes. |
 |
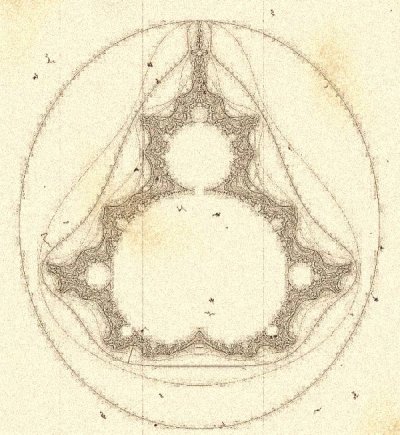
Fractals Het gebruiken van een getal tussen 1 en 2 is ook de basis van de moderne fractale meetkunde. In 1967 schreef BenoÓt B. Mandelbrot het geruchtmakende artikel 'How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension'. Hij stelde vast dat hoe nauwkeuriger je naar de kust kijkt, hoe langer en gedetailleerder de kustlijn wordt. Mandelbrot bewees dat kustlijnen en andere geografische grenzen een dimensie hebben die ook tussen 1 en 2 in ligt. In zijn boek 'The fractal geometry of nature' (1982) werkte hij dit verder uit. Uit zijn opvattingen over dimensies ontwikkelde Mandelbrot een bijdrage aan de theorie van fractals, objecten met een gebroken dimensie. Een fractal is een wiskundige figuur waarvan de onderdelen gelijkvormig zijn met het geheel. Op allerlei plekken in zo'n figuur komt men een soort Droste-effect tegen. Fractale wiskunde droeg weer bij tot de vorming van de chaostheorie. Mandelbrot 'ontdekte' de fractal, maar in wezen had Da Vinci die ontdekking al veel eerder gedaan. Bestudering van de geheime aantekeningen in de Codex Leicester leert dat hij al vroeg bezig was fractals te creŽren. Gates heeft deze aantekeningen angstvallig geheim gehouden, waarschijnlijk omdat er in de code nog nieuwe, toepasbare principes van de computer verstopt zouden zijn, maar daarmee houden wij ons nu niet bezig. Een voorbeeld van de zogenaamde Mandelbrot fractal zien we in de bijgaande afbeelding. Daaruit blijkt dat Da Vinci al in de late vijftiende eeuw dergelijke constructies maakte. Kennelijk was het genie van de renaissance ook op dit gebied zijn tijd voor. |
 |
|
|
Ook de fractal met het 'stof' van Cantor, "Cantor dust" genoemd, was bij Da Vinci bekend. Daarbij wordt een vierkant in 16 gelijke delen verdeeld, waarvan er 4 worden vervangen door 4 vierkanten, die ieder telkens weer in 16 delen worden opgedeeld. En zo verder. Als men de punten die daarvan het resultaat zijn, allemaal op een rij zet, krijgt men een lijnstuk met de dimensie 1. In het werk van da Vinci komt af en toe zo'n lijn voor, bijvoorbeeld de horizontale tafelrand in Het laatste avondmaal. |
Na Leonardo nam de belangstelling voor getallen tussen 1 en 2 af. Fermat noteerde er een stelling over maar deze had een negatieve strekking. Hij formuleerde: 'Voor elk geheel getal n tussen 1 en 2 heeft de vergelijking xn+yn=zn geen oplossingen'. Het bewijs daarvoor schreef hij in de marge van zijn aantekeningenboek, zodat er te weinig ruimte overbleef voor het bewijs van zijn laatste stelling. Pas in de negentiende eeuw construeerden Gauss en Riemann vormen van wiskunde waarin 1 + 1 niet 2 was maar 1,617. Zijn de tekeningen van het Mandelbrot-mannetje door Da Vinci niet terug te voeren op toeval? Dat zou misschien het geval zijn als Leonardo niet nog een gedetailleerde fractal had gemaakt. De sluitsteen van het bewijs vinden we in een fractale vorm die genoemd is naar de wiskundige Raymond Julia. Deze klassieke Julia-fractal komen we namelijk ook in de Codex Leicester tegen. Hieruit blijkt maar weer dat ook op wiskundig gebied Da Vinci een groot genie van de renaissance was. |  |
