Back to Main Index
Fractalary: Fractals from Planets to
Atoms
Patent Application (The Netherlands) by Julius J.C.M. Ruis,
number 10 33 147 d.d. 29 December 2006
The use of Fractal Geometry in Rapid
Prototyping and Tissue-Engineering
of artificial human organs, more
specifically human blood vessels
Click
here for prototype artificial blood vessel |
|||||
Julia Set
|
Mandelbrot Set
|
Julius Ruis Set
|
|||
|
|
|
|
|||
|
Introduction
and summary What is a
Fractal? A fractal is a geometric object (like a line
or a circle) which is however rough or irregular on all scales of length, and
so which appears to be 'broken up' in a radical way. Some of the best
examples can be divided into parts, each of which is similar to the original
object. Fractals are said to possess infinite detail, and they may actually
have a self-similar structure that occurs at different levels of magnification.
The most well-known fractals are the Mandelbrot Set and Julia Sets. Jules
Ruis developed the so called Julius Ruis Set. This is a smart presentation of
400 Julia sets, showing that the Mandelbrot Set is the parameter basin of all
closed Julia Sets. Why Fractal
Geometry? Fractals provide scientists with a new
vocabulary to read the book of nature. Galileo's circles and triangles are
insufficient to describe nature in all its rugged complexity. In addition,
the fact that natural objects are commonly self-similar, makes fractals ideal
models for many of those objects. Fractal geometry also provides scientists
with a new way of looking and experimenting with old problems using a
different perspective. What is most exciting about fractals is that they
successfully bring geometry to where it did not appear to belong, an idea
reminiscent of general relativity, which is based on the introduction of
geometry to understand the cosmos. What is Fractal
Geometry good for? Fractal geometry is a
compact way of encoding the enormous complexity of many natural objects. By
iterating a relatively simple construction rule, we see how an original
simple object can be transformed into an enormously complex one by adding
ever increasing detail to it, at the same time preserving affinity between
the whole and the parts, or scale invariance. Just think of a big oak tree in
winter. Its branches are naked so it is easy to distinguish the way in which
a twig splits and becomes two which then split again, to become four; in much
the same way in which the trunk first split into slender branches which split
again and then again, and again. The self-similarity is evident, the whole
looks just like its parts, yet not exactly. Nature has slightly altered the
construction rule, introducing some degree of randomness which will make one
oak slightly different from any other oak tree in the world. Now, imagine packing
all the information required by the tree to become a beautiful large oak tree
into the smallest possible space, with the greatest economy of means. It
would appear logical that rather than encoding all the unique, intricate
complex branching of a mature oak in its seed (an acorn), all the details of
its evolving shape, nature simply encodes the splitting rule, and the urge to
repeat it, to iterate. This, plus a little randomness during growth that
changes the number of splits or their place in a branch is enough to create a
unique oak tree. In fact a whole computer data compression industry is based
on similar ideas that permit coding and compressing large files to be quickly
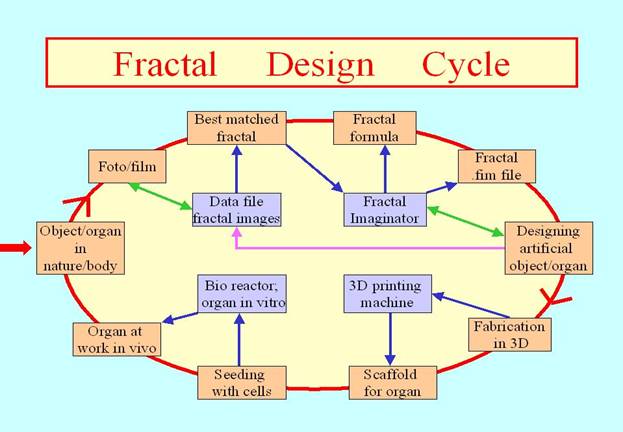
transmitted through the Internet. Patent application Jules Ruis, managing
director of Fractal Consultancy (The Netherlands), filed end 2006 a patent
application on a procedure using fractal geometry for the design and
manufacturing of artificial human and/or animal organs, more specifically
human blood vessels. The designed structures can be presented in a
two-dimensional as well as a three-dimensional way. The patent pending also
emphasizes the use of fractal geometry for the direction of print- and
injectionheads in equipment used for the application of materials (inkjet
printing and methods of direct writing), and equipment that directs
laserbeams and electronic beams (electron microscopes). More information Jules Ruis, Fractal
Consultancy, Son-Eindhoven, The Netherlands, tel. +31 499 47 10
55; internet: www.fractal.org e-mail: Jules.Ruis@fractal.org
|
|||||
|
Content 1. Fractal
Design Cycle 2. The
Fractal Nature of Nature (from Planet to Atoms) 3. Fractal
Images of Human Organs 4. Print
me a Heart and a Set of Arteries 5. Fractal
Structure of DNA and smaller particles |
|||||
|
|
|||||
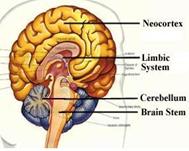
Main Index of examples Nature/Body
-
Universe -
Milky Way and
the sun -
Sun and its
planets -
Earth -
Clouds/mountains/rivers
-
Butterfly/zebra/peacock -
Pyramid/Sagrada
familia -
Dicentra
spectabilis/cactus -
Fungus/flower/cauliflower -
Tree -
Human body and
organs -
Brain/eye/ear/ -
Heart/blood
vessel/lungs -
Digestion/intestines/liver -
Stomach/colon/kidneys -
Bladder/trabecular
bone -
Cell/neuron/mitochondrium -
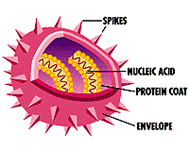
Bacterium/virus -
DNA/RNA/protein
-
Dendrimer -
Molecule/atom/particle -
Unparticles |
Fractal
Geometry -
Fractal
Geometry is the iteration of complex functions like (inverted) polynomials (z2, z3, etc) and complex (inverted)
transcendental functions (sin(z), cos(z), tan(z), exp(z) ). -
A complex
number has the form z=x + i*y or c=a + i*b with i2
=-1 -
In fractal
formulas zn+1 means z(new) and zn
means z(old). -
Formula
in function is iterated from 1 to maximal ‘k’ times. -
Iteration goes
on until predeter-mined small/great value has been reached (function is going
to zero or infinity). -
Quantity of
real done iterations is called ‘f’ (‘flightnumber’). -
Instruction at
the end of the procedure, coupled on reached ‘f’, is : pset color, position
machine printhead (ink, matter, cell or molecule, etc), manipulate
beam/bundle or position motor. -
Calculate next
computer-pixel and manipulate next machine-voxel, layer for layer. |
Fractal Imaginator
- The Fractal Imaginator is a software program to create fractals. - Using the program Fi you can input your own mathematical formulas and
other relevant data. - The created images are saved as bmp/jpg/png files or obj/stl/pov
files. - The parameters of the image are stored in separated data-files (.fim
files). - This way of storing saves much computer capacity. -
After installation of Fi on your
own computer the Fi program will automatically start by clicking the .fim
files (just like Adobe pdf files). -
Buy program: -
http://www.mysticfractal.com/FractalImaginator.html -
Download free
trial version: |
|||
|
|
|||||
The fractal nature of nature, from planet
to atoms
The Universe as a Fractal Space
|
|||||
|
|||||
|
http://www.fractal.org/Bewustzijns-Besturings-Model/Fractal-Nature.pdf |
|||||
|
|
|||||
|
|
|
-
Is the
Universe a Fractal Space ? -
Article in New
Scientist d.d. 9 March 2007: -
http://www.fractal.org/Bewustzijns-Besturings-Model/Is-the-universe-a-fractal-space.htm
-
For fractals
in general see: |
|||
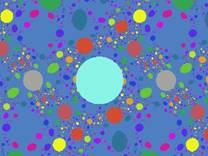
Univers
|
Julia:
zn+1 = zn2
+ c (iteration
= 200) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Univers.fim |
|||
|
|
|
|
|||
|
|
|
- The Milky
Way system is a spiral galaxy consisting of over 400 billion stars , plus
gas and dust arranged into the halo, the nuclear bulge and the disk, which
contains the majority of the stars, including the sun. -
The best fractal formula for a spiral is zn+1 = zn2 + c at a point with x>0 and small y=0,04 |
|||
Milky Way and the Sun
|
Julia: zn+1 = zn2 + c (iterations = 300) |
Http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Spiral.fim
|
|||
|
|
|
|
|||
|
|
|
-
The Sun
possesses 9 planets: Pluto, Neptune, Uranus, Saturn, Jupiter, Mars, Earth,
Venus and Mercury. -
On earth we
see much more celestial bodies at the starry sky. -
Only the
tan-functions give the fractal structure with balls. |
|||
Sun and its planets
|
Julia: zn+1 = tan(zn) * c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/sun.fim |
|||
|
|
|
|
|||
|
|
|
-
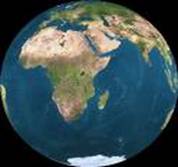
The Earth
is the only planet of the sun on which Life is possible. -
The inner side
of the earth consists out of 4 different layers. -
See also
Google Earth -
The showed
fractal is the ‘superformula’ near c=0 with iterations=215 |
|||
Earth
|
Julia: zn+1 = 1/(cos(zn)2 -sin(zn)2)^(5) + c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/earth.fim |
|||
|
|
|
|
|||
|
Benoit
Mandelbrot: "Clouds
are not spheres, mountains are not cones, coastlines are not circles, and
bark is not smooth, nor does lightning travel in a straight line." |
|||||
|
|
|||||
|
|
|
|
|||
|
Clouds and mountains |
River
|
Trees
|
|||
|
|
|
|
|||
|
|
-
The Pyramids
in Egypt were constructed as images of the stars at the sky. -
So a
connection was realised between heaven and earth. -
Maybe the
pyramids were the first sign of the fractal structure of space. -
The so called Sierpinski
fractal looks like a pyramid. |
||||
Pyramid of Cheops
|
Julia: if (x>=0) then zn+1=( zn-1) * c, else zn+1
=
(zn +1) * conj.c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Pyramid.fim |
|||
|
|
|
|
|||
|
|
|
-
La Sagrada
Familia
(Cathedral in Barcelona) was developed by Gaudi. -
The
architectural design (inside and outside) is completely nature-inspired
(=fractal). -
The complex
transcendental functions, especially the sine and cosine, give the best
impression of this man-made construction. |
|||
|
Sagrada Familia (Barcelona) |
3D Juliaquat: zn+1 = sin(zn) * c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Sagrada.fim |
|||
|
|
|
|
|||
|
Animals and repeating patterns
|
|||||
|
|
|
|
|||
Butterfly
|
Zebra
|
Peacock
|
|||
|
|
|
|
|||
|
|
|
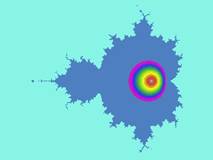
-
The middle
fractal is the image of the most popular fractal: the Mandelbrot Set
(after the Polish Frenchman Benoit Mandelbrot ). -
Zooming in at
the border of the fractal gives new mini-M-sets. -
The M-set
looks like the left showed flower, called the dicentra spectabilis (in Dutch:
broken heart). |
|||
Dicentra spectabilis
(gebroken hartje) |
Mandelbrot: zn+1 = zn2 + c for c=(0,0) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Mandel-z2.fim |
|||
|
|
|
|
|||
|
|
|
||||
Cactus
|
Julia: zn+1 = zn2 + c for c = (-1,0) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Julia-set.fim |
|||
|
|
|
|
|||
|
|
|
-
The middle
fractal is the so called Julius Set: a smart presentation of 400 Julia
sets, showing that the Mandelbrot set is the parameter basin of all closed
Julia sets. -
The whole is
reflected in each part. Each part is projected in the whole. See showed set
of cacti at the left. |
|||
Set of cacti
|
Julius: zn+1 = zn2 + c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Julius-z2.fim |
|||
|
|
|
|
|||
|
|
|
-
Julia sets can
be showed with and without external orbits. -
Julia sets
with external orbits get the addition ‘Ruis’ (i.e. ‘noise’). -
A Julius set
can be shown as 400 Julia sets with orbits. This set is called a Julius
Ruis Set (after Jules Ruis from The Netherlands). |
|||
Plant dicentra spectabilis
|
Julius Ruis: zn+1 = zn2 + c |
See for complete Julius Ruis
Gallery: http://www.fractal.org/Julius-Ruis-Gallery/Index-Gallery.htm |
|||
|
|
|
|
|||
|
|
|
-
The fungus is
an example of the form that belongs to the exponential functions. -
A repeating
pattern can be found along the y-axis, so x=0, especially on y-values that
are multiplications of pi (=3,1415). -
In many cases
mathematical fractals show an attractor. This are special points, with
moving orbits around it, like a rainbow. |
|||
|
Fungus |
Mandelbrot: zn+1 = exp(zn) * c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Mandel-exp.fim |
|||
|
|
|
|
|||
|
|
|
-
Formulas for inverted
sine and cosine are very suitable for the creation of fractal flowers. -
A special
‘superformula’ has been developed by Jules Ruis.. -
The number of
leaves is equal to the power of the sine/cosine. -
The colours
can be changed by a special parameter. |
|||
Flower
|
Julia: zn+1 = c / ( (cos(zn)2)-
(sin(zn)2))^5 (power = 10) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Flower.fim
|
|||
|
|
|
|
|||
|
|
|
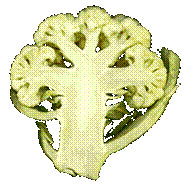
-
Cauliflowers, broccoli and romansco are
examples of food with a typical fractal tree-like structure. -
The fractal
image is constructed with a so called ‘if-then-else’ formula. -
The branches
on the stem originate from the power of two for (zn -1) or (zn+1). |
|||
|
Cauliflower |
Julia: if (x>=0) then zn+1 = ((zn -1)2) / c, else zn+1 = ((zn +1)2) / conj.c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/r8^2.fim |
|||
|
|
|
|
|||
|
|
|
||||
Tree
|
Julia: if x>0 then zn+1 = (zn +1)/c else zn+1
= (zn -1)/conj.c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Tree-it=10.fim |
|||
|
|
|
|
|||
Fractals support growing organs
Today scientists can regenerate tissue such as skin,
but they are still figuring out how to grow replacement organs. The challenge
is in coaxing cells from organs to grow into new organs rather than
unstructured clusters of cells.
|
Researchers found a way to impart structure to growing
cells that may eventually allow for growth of entire organs. If the method proves successful, "we can use [a]
patient's own cells to create a living organ and this will remove the
problems with organ rejections" and a shortage of donor organs, said
Mohammed Kaazempur-Mofrad, a researcher at MIT
|
The researchers used computer-generated fractal
patterns to fabricate a network of branching, microscopic tubes. Fractals are
patterns that repeat at different scales. If, for instance, one portion of a
fractal looks like a tree, zooming in on its branches and twigs will show
that they also look like trees, and zooming further will show that their
branches and twigs follow the same pattern. See article: http://www.fractal.org/Life-Science-Technology/Publications/Fractals-support-growing-organs.htm |
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
||||
Human body within a body
|
Julia Ruis: zn+1
= c / (zn3 + zn2 – zn) (inverted
polynomial) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/cdiv-poly.fim |
|||
|
|
|
|
|||
|
|
|
|
|||
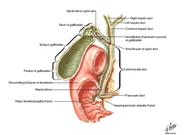
Human organs
|
25 *
Julia: if x>0 then zn+1 = (zn +1)/c else zn+1 = (zn -1)/conj.c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/if-then-JR5.fim |
|||
|
|
|
|
|||
|
|
|
Using
Fractal Geometry for Rapid Prototyping and Tissue Engineering -
Fractal
geometry is used for rapid prototyping of so called scaffolds. -
Middle photo
shows tree-like scaffolds (negative and positive) used for the creation of
artificial blood vessels. -
Biodegradable
polymer scaffolds are seeded with endothelial cells and conditioned ‘in
vitro’ in a bioreactor (Tissue Engineering). -
After some
weeks the artificial organ will be placed in human body and natural growth
starts. |
|||
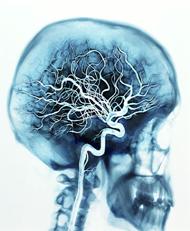
Brain blood vessels
|
3D
scaffold in wax; Juliaquat: if x>0 then zn+1 = (zn +1)/c else zn+1
=
(zn -1)/conj.c |
||||
|
|
|
|
|||
|
|
|
Fractal Dimension
-
The dimensions
of objects in euclidean mathematics are 1, 2 or 3 (resp. line, surface and
content). -
The fractal
dimension is a non-integer e.g. 2,79 for the surface of the brain. -
Due to the
patented invention no CAD-files are needed any longer for printing 3D forms. |
|||
Brain surface
|
3D Juliaquat: if (x>=0) then zn+1 = (zn -3)/c, else zn+1
= (zn+3)/conj.c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Tree-quat.fim |
|||
|
|
|
|
|||
|
|
|
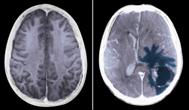
- Healthy
brain (left) compared to brain tumor (shown in blue, right). - There are
many types of brain tumors. -
Fractal formula is zn-2 without
brackets around ‘-2’. |
|||
|
Brain and malignant brain tumor |
Julia: zn+1 = zn-2+ c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/malignant-tumor.fim |
|||
|
|
|
|
|||
|
|
|
-
Polynomials
near tot the point c=0 look like a mandala. - Each mandala possesses three
repeating characteristics: *centre * symmetry * essential
points - The eye retina looks like a
mandala fractal structure. |
|||
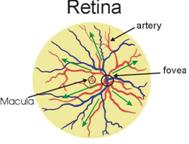
Eye Retina
|
Julia: zn+1 = zn6 + c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/z6-core.fim |
|||
|
|
|
|
|||
|
|
|
-
Several
objects in nature (shells etc.) have a spiral form. -
Also human
ears possess a spiral ‘cochlea’ inside the head. -
A spiral is
related to the figure phi; phi = 1,618 i.e. the Golden Ratio. -
This ratio is
derived from the Fibonaccio set of numbers: 1, 2, 3, 5, 8, 13, 21, 34, 55,
………. -
Each next
number is the addition of the two former numbers. -
The division
of a number by its former number delivers always the result of phi. -
The showed 3D
fractal is constructed with formula of sin(z) and subtraction of sinh(z). http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Quat-ear.fim |
|||
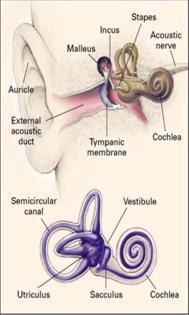
Ear and its inner structure
|
3D
Juliaquat: zn+1 = (sin(zn) - sinh(zn)+c and Julia: zn+1 = zn2 + c |
||||
|
|
|
|
|||
|
|
|
-
Complex sine
and cosine are the most suitable functions for the design and construction
of 3D artificial blood vessels. -
A special ‘superformula’
has been developed. -
Scaffolds are
printed with biodegradable polymers. -
Methods of
‘Direct Write’ are under development. |
|||
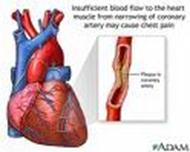
Heart and its blood vessels
|
3D Juliaquat: zn+1 = c / (cos(zn)2 - (sin(zn)2)^(2) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Julia-cdivsuper.fim |
|||
|
Print me a heart and a set of arteries (publication
d.d. April 2006) www.fractal.org/Fractal-Research-and-Products/Print-arteries.mht Sitting in a culture dish, a layer of chicken heart cells beats in
synchrony. But this muscle layer was not sliced from an intact heart, nor
even grown laboriously in the lab. Instead, it was "printed", using
a technology that could be the future of tissue engineering. Gabor Forgacs, a
biophysicist at the University of Missouri in Columbia, described his
"bioprinting" technique last week at the Experimental Biology 2006
meeting in San Francisco. It relies on droplets of "bioink", clumps
of cells a few hundred micrometres in diameter, which Forgacs has found
behave just like a liquid. This means that
droplets placed next to one another will flow together and fuse, forming
layers, rings or other shapes, depending on how they were deposited. To print
3D structures, Forgacs and his colleagues alternate layers of supporting gel,
dubbed "biopaper", with the bioink droplets.
To build tubes that could serve as blood vessels, for instance, they lay down
successive rings containing muscle and endothelial cells, which line our
arteries and veins. "We can print any desired structure, in
principle," Forgacs told the meeting. Other tissue engineers
have tried printing 3D structures, using modified ink-jet printers which
spray cells suspended in liquid (New Scientist, 25 January 2003, p
16). Now Forgacs and a company called Sciperio have developed a device with
printing heads that extrude clumps of cells mechanically so that they emerge
one by one from a micropipette. This results in a higher density of cells in
the final printed structure, meaning that an authentic tissue structure can
be created faster. Cells seem to survive
the printing process well. When layers of chicken heart cells were printed
they quickly begin behaving as they would in a real organ. "After 19
hours or so, the whole structure starts to beat in a synchronous
manner," says Forgacs. Most tissue engineers
trying to build 3D structures start with a scaffold of the desired shape,
which they seed with cells and grow for weeks in the lab. This is how Anthony
Atala of Wake Forest University in Winston-Salem, North Carolina, and his
colleagues grew the bladders which he successfully implanted into seven
people (New Scientist, 8 April 2006, p 10). But if tissue engineering
goes mainstream, faster and cheaper methods will be a boon. "Bioprinting
is the way to go," says Vladimir Mironov, a tissue engineer at the
Medical University of South Carolina in Charleston. |
|||||
|
|
|||||
|
|
|
|
|||
|
|
|
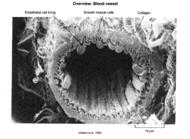
-
The left photo
shows the internal (and external) anatomy of a blood vessel and has been
artificial designed (fractal in the middle). -
The used
function is an inverted polynomial. -
The number of
furrows depends on the power of the function. -
Walls
thickness is determined by the number of iterations. |
|||
Blood vessel anatomy
|
Julia: zn+1 = zn-2 + c (iterations = 8) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Julia-z^-2-it=8.fim |
|||
|
|
|
|
|||
|
|
|
-
The lung
is the best example of a tree-structured organ in human body. -
The middle
image is a stem with branches. -
The tree is
constructed with the so called ‘if-then-else’ function. -
The number of
branches depends on the quantity of iterations. |
|||
|
Lungs and its branches [1] |
Julia: if x>0 then zn+1 = (zn +1)/c else zn+1
= (zn -1)/conj.c (it. = 7; without orbits) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/stem-it=7.fim |
|||
|
|
|
|
|||
|
|
|
-
The lung in
more detail still shows a fractal form. -
The color is
created by setting on the orbits-parameter. -
Each branch
has its own color following the color-spectrum. -
The number of
branch-bifurcations has been increased by changing the number of
iterations. |
|||
Lungs and its branches [2]
|
Julia: if x>0 then zn+1 = (zn +1)/c else zn+1
= (zn -1)/conj.c (it. = 10; with orbits) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/stem-color-it=10.fim |
|||
|
|
|
|
|||
|
|
|
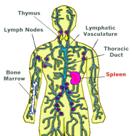
-
The spleen
is similar to a lymph node in shape and structure but is much larger. In
fact, it is the largest lymphatic organ in the body. It is
responsible for the destruction of old red blood cells. It is a major
site for mounting the immune response. |
|||
|
Spleen and lymphatic system |
|
|
|||
|
|
|
|
|||
|
|
|
-
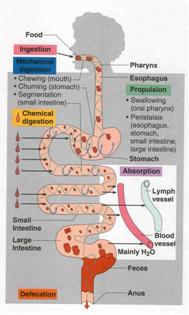
Digestion
and intestines from mouth to anus. -
The so called
‘Superformula’ has been developed for the creation of different kind of
tubes, usable for gullet and colons. |
|||
Digestion and intestines
|
3D Juliaquat: zn+1 = c * (cos(zn)2 - sin(zn)2)^(2) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/quatjulia-c-super-JR5.fim |
|||
|
|
|
|
|||
|
|
|
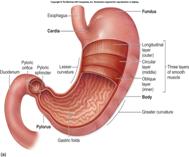
- The stomach
is the first stop for the food after the esophagus. - Once the
food gets to the stomach the stomach uses chemicals to try to make the food
tinier. -
The showed fractal is a special so called ‘if-then-else’ formula for
x#>x. -
The fractal is a 3D construction (i.e. .obj or .stl file) |
|||
Stomach
|
3D Juliaquat: if (x#>x) then zn+1 = (zn -1) * c, else zn+1 = (zn +1) * conj.c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Stomach.fim
|
|||
|
|
|
|
|||
|
|
|
-
The liver
is used for the creation of chemicals for breaking off the food. -
The used
formula is the standard ‘if-then-else’ formula for a tree. -
We distinguish
two kinds of bloodvessels: arteries (coming from the heart) and veins
(going to the heart). |
|||
Liver
|
Julia: if x>0 then zn+1 = (zn +1)/c else zn+1
= (zn -1)/conj.c (without orbits) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Tree.fim |
|||
|
|
|
|
|||
|
|
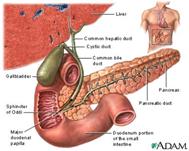
- The pancreas
is located behind the liver and is where the hormone insulin is produced. - Insulin is used by the
body to store and utilize glucose. -
|
||||
|
Pancreas |
|
|
|||
|
|
|
|
|||
|
|
|
- The liver
produces bile which aids in the digestion of fats. The bile travels
through tiny canals which eventually drain through the common bile duct into
the small intestine. -
The gallbladder stores excess bile that is not immediately needed
for digestion. |
|||
|
Gallbladder |
|
|
|||
|
|
|
|
|||
|
|
|
-
The small
intestine is the part of the gastrointestinal tract between the stomach
and the large intestine and comprise the duodenum, jejunum and ileum.
It is where the vast majority of digestion takes place. -
The fractal
formula is a Julia set of a standard polynomial with orbits. |
|||
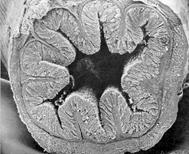
|
Small intestine structure |
Julia: zn+1 = zn12 + c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Start-z^12.fim |
|||
|
|
|
|
|||
|
|
|
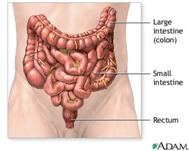
- The large
intestine or colon, is a muscular tube that begins at the end of the
small intestine and runs to the rectum. The colon absorbs water from liquid
stool that is delivered to it from the small intestine. -
The fractal formula for the 3D Julia set is the ‘if-then-else’ formula
for (z+1) or (z-1). |
|||
Intestine
|
3D Juliaquat: if x>0 then zn+1 = (zn +1)/c else zn+1
= (zn -1)/conj.c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/if-then-z+1-quat.fim |
|||
|
|
|
|
|||
|
|
|
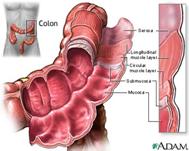
- The colon
is a long hollow organ lined with mucous membrane (mucosa). Muscle layers
wrap around the entire length and help move food material through to the
rectum. - The fractal
formula used is the so called inversed superformula. -
The showed image is a 3D presentation. |
|||
|
Colon structure |
3D Juliaquat: zn+1 = c / (cos(zn)2 - (sin(zn)2)^( 2) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Colon.fim |
|||
|
|
|
|
|||
|
|
|
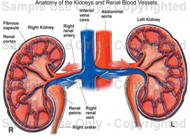
- The kidneys
are ‘bean-shaped’ organs. -
The kidneys filter wastes from the blood and
excrete them, along with water as urine. -
The showed images are two turned fractal trees with the
‘if-then-else’ structure. |
|||
Kidneys
|
2 *
Julia: if x>0 then zn+1 = (zn +1)/c else zn+1 = (zn -1)/conj.c (with orbits) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/cdiv-z^2-z-quat.fim |
|||
|
|
|
|
|||
|
|
|
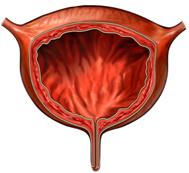
- The bladder
has an outer wall of muscle and connective tissue - Nerves in
the wall monitor bladder filling and signal the body to urinate. - Like other
organs the bladder's inner surface is lined with epithelial cells. - The formula
for the fractal image is an subtraction of two polynomials, one for the
circle and one for the inverted z^2. -
Also the internal structure of the fractal has a beautiful shape. |
|||
Bladder
|
3D Juliaquat: zn+1 = c * zn - (1/zn2 * c) |
Http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Bladder.fim |
|||
|
|
|
|
|||
|
|
|
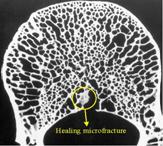
- The overall
architecture of bone is divided into inside cancellous bone (also referred to
as trabecular bone) and cortical bone (shell). -
Trabecular bone has a branching pattern, as seen in the vertebral
specimen (left image). -
For more details see: |
|||
Trabecular bone
|
3D Juliaquat: if (x>=0) then zn+1 = (zn -1)/c, else zn+1
= (zn +1)/conj.c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Bone.fim |
|||
|
|
|
|
|||
|
|
|
-
An ovum
is a female reproductive cell. This cell is the largest cell in human body. -
The middle
image is a fractal made of tan(z) on the position a=0 and b=3,298575 -
The exp(z)
gives also a repeated pattern on the y-axis on multiplied positions of
1/10 pi (0,31415) |
|||
Ovum (egg cell)
|
Julia: zn+1 = c * tan (zn) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/ctanz.fim |
|||
|
|
|
|
|||
|
|
|
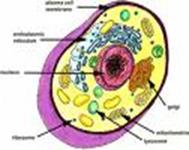
-
The human cell
consists of a nucleus embedded in cytoplasm and surrounded by a
membrane. -
Different
organelles are driving in the cytoplasm. e.g. the mitochondria that
are the ‘power factories’ of the cell. -
The fractal
formula for the middle image is a polynomial divided by another polynomial. |
|||
Animal/human cell
|
Julia: zn+1 = (3 * (zn3 +
3)/(2 *(zn5
–5 ) * c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Cell.fim |
|||
|
|
|
|
|||
|
|
|
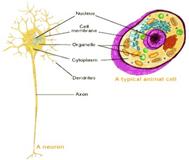
- Neurons
(also known as nerve cells) are electrically excitable cells in the nervous
system that process and transmit information. - Neurons are typically
composed of a soma, or cell body, a dendritic tree and an axon. -
The fractal formula is of the form ‘if-then-else’ composed with
sin(n)+1 and sin(n)-1. |
|||
|
Neuron (dendrites and axon) |
Julia:
if x>0 then zn+1 = (sin(zn)+1)/c else zn+1 = (sin(zn)-1)/conj.c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/if-then-sin.fim |
|||
|
|
|
|
|||
|
|
|
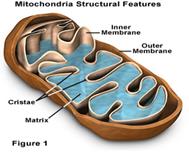
-
Mitochondria are complex organelles that convert energy from
food into a form that the cell can use. They have their own genetic material,
separate from the DNA in the nucleus. -
Analysis of
the mtDNA (about 16.000 base-pairs of nucleotides) let us see that the
mtDNA is fractal structured. |
|||
Mitochondrium
|
Julia: zn+1 = 1 / (zn6+ c) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Mito.fim |
|||
|
|
|
|
|||
|
|
|
- Bacteria are
prokaryotes. Unlike animals and other eukaryotes, bacterial cells do not
contain a nucleus or other membrane-bound organelles. - It has many
shapes including spheres, rods, and spirals. -
The fractal formula is a special composition of cos(n) multiplied with
a polynomial. |
|||
Bacterium
|
Julia: zn+1 = cos(zn) * zn2.5 + c (zoomed in) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Bacterium.fim |
|||
|
|
|
|
|||
|
|
|
-
A virus can infect the cells of a biological organism. They
cannot reproduce on their own. -
Their surface carries specific tools designed to cross the barriers of
their host cells. -
The fractal formula for the virus and the bacterium is the same. -
Zooming in and out creates the difference. |
|||
Virus
|
Julia: zn+1 = cos(zn) * zn2.5 + c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Virus.fim
|
|||
|
|
|
|
|||
|
Andras
Pellionisz (International PostGenetics Society):
“My
knowledge of the universe is almost nil; 40+ years of research and 3 Ph.D.-s
in Computer Engineering, Biology, and Physics don't measure up to the
universe. However, having devoted the most recent 7 years entirely to the
deep study of the DNA, I have evidence that the DNA is fractal. Perhaps not
surprisingly, since it is a rather conspicuous tiny part of the universe.” |
|||||
|
|
|
- DNA is a
double helix formed by base pairs attached to a sugar-phosphate backbone. -
DNA can also be found in the mitochondria. This mtDNA is fractal structured. http://www.fractal.org/Fractal-Research-and-Products/Fractal-Structure-mtDNA.pdf |
|||
DNA
|
Julia:
zn+1 = c * (cos(zn)2 - sin(zn)2)^(2) |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/DNA-dh.fim |
|||
|
|
|
|
|||
|
|
|
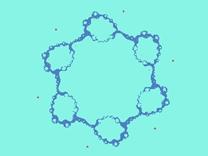
-
Dendrimers are macro-molecules that are made
up of branching molecules joined together. -
The fractal
structure is realised with polynomials with the c-value near to zero. |
|||
|
Dendrimer |
Julia: zn+1 = zn2 + c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/dendrimer.fim
|
|||
|
|
|
|
|||
|
|
|
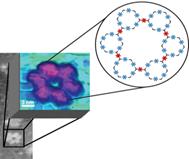
- A molecule
is a group of atoms in a definite arrangement held together by chemical
bonds. -
Scientists have created and captured a
man-made molecule at the nanoscale. -
It shows a fractal structure. -
The geometric
fractal was made with a formula for the inverted polynomial z^-6 |
|||
Man-made molecule
|
Julia: zn+1 = zn-6+ c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/z^-6.fim |
|||
|
|
|
|
|||
|
|
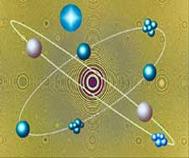
|
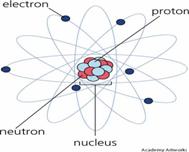
-
Atoms are the building blocks of the
molecules. -
Each atom
consists out of a nucleus with protons and neutrons. -
Electrons are moving in 8 orbits around the
nucleus. -
See Periodic
Chart of Elements: |
|||
Atom
|
Julia: zn+1 = zn6 + c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/z6-start.fim |
|||
|
|
|
|
|||
|
|
|
- There are 2
types of subatomic elements: fermions which make matter and bosons
which make forces. - Each element
is as well particle as wave, depending of the eye of the beholder. -
The fractal orbits of z^6 can be influenced by the external
‘flightnumber’ going to infinity. |
|||
Subatomic particles
|
Julia: zn+1 = zn6 + c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Particles.fim |
|||
|
|
|
|
|||
|
|
|
-
Unparticles, but not particles, can fit in a theory that
has the property of continuous scale-invariance, which is to
visualize by fractal images (iterating complex functions). -
A fractal like this Koch Curve is an example of discrete
scale-invariance because it looks the same if multiplied by a fixed number. |
|||
Unparticles
|
Julia: if (x>=0) then zn+1 = (zn -1)*c, else zn+1
= (zn +1)*conj.c |
http://www.fractal.org/Julius-Ruis-Gallery/Fractalary/Koch-2.fim |
|||
|
|
|
|
|||
|
The quadratic iteration of the Mandelbrot set [King] compared with the
interactive effects of inverse quadratic charge interaction in tissues
[Campbell]. |
|||||
|
|
|||||
|
© Chris King, 2007 The quadratic iteration of the Mandelbrot set [King] compared with the
interactive effects of inverse quadratic charge interaction in tissues
[Campbell]. Although
their genesis arises from differing non-linear process, iteration on the one hand
and interaction on the other, the multi-fractal structures of tissues have
features similar to the Mandelbrot set on changes of scale. These fractal
effects reach from the molecular (a) in which individual proteins are illustrated
embedded in the lipid membrane, through cell organelles (b) to the
intercellular structure of whole organs as illustrated by skin (c). Such scale-dependent
coherence of structure is possible only because of the highly nonlinear
nature of the electromagnetic force in quantum charge interactions of
fermionic matter. |
|||||